We have divers methods of Approximation delivered by Wallis, Raphson, Halley, Howard, etc., all of them being no other than Series's infinitely converging, or approaching still nearer to the Quantity required, according to the Nature of the Series.
See CONVERGING and SERIES.
'Tis evident, that if a number proposed be not a true Square, it is in vain to hope for a just quadratic Root thereof, explicable by rational Numbers, integers or fractioned; whence, in such Cases, we must content ourselves with Approximations, somewhat near the Truth, without pretending to Accuracy: and so for the Cubic Root, of what is not a perfect Cube; and the like for superior Powers.
See SQUARE, CUBE, POWER, QUADRATURE, EXTRACTION, etc.
This the Ancients were aware of, and accordingly had their Methods of Approximation; which, though scarcely applied by them beyond the quadratic or perhaps the cubic Root, are yet equally practicable, by due Adjustments, to the superior Powers also: as is shown in the Philosophical Transactions, No 215.
If there be a Non-quadratic or Non-cubic Number;
the former being expressed by aa + b, and the latter by aaa + b,
where aa and aaa are the greatest Square and Cube in the proposed Numbers;
then √(aa + b) = a + ( ab / (2aa + ½ b ) )
and √(aaa + b) = a + ( ab / (2aaa + b ) ) = a + √(¼aa) + (b / 3a)
will be easy and expeditious Approximations to the Square and Cube Root.
To extract the Root of an Equation by Approximation:
1°. For a quadratic Equation—suppose the Equation x^2 - 5x - 31 = 0 ;
let the Root be 8 + y, so that y may denote the Fraction, whereby the assumed Number either exceeds or comes short of the Root:
Then
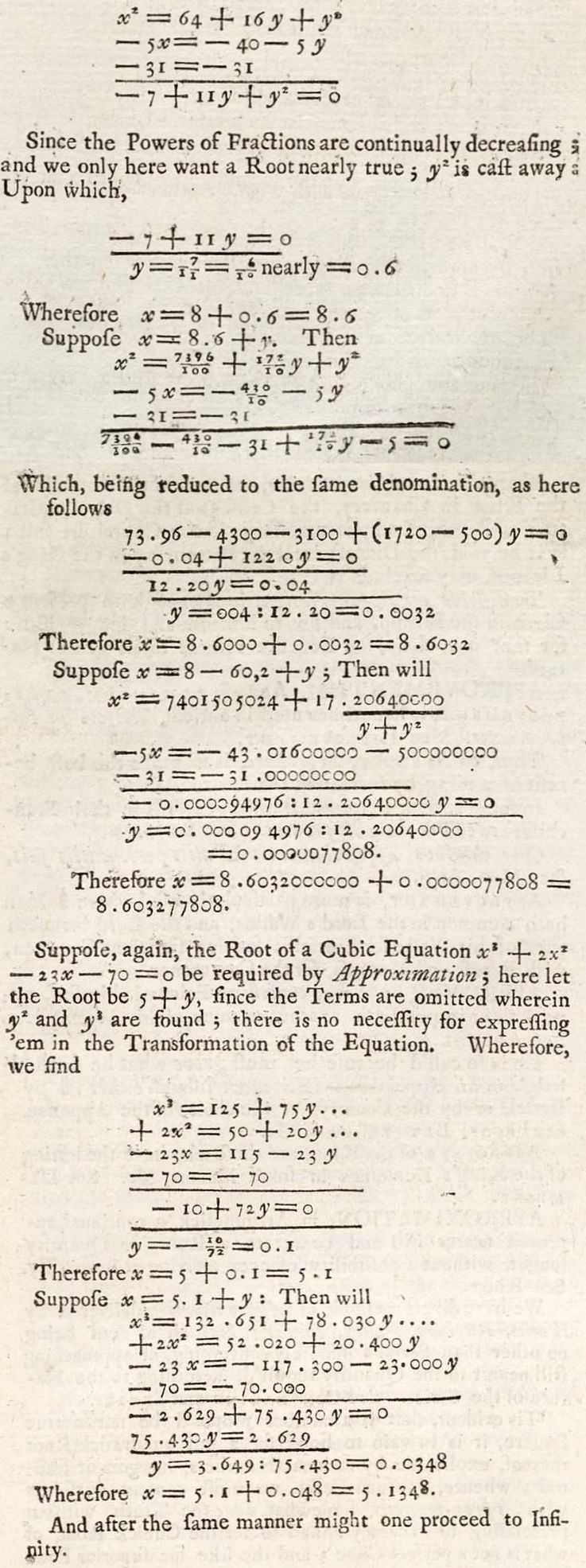
And after the same manner might one proceed to Infinity.
