In this sense we say the axis of a sphere, or globe; the axis, or axle-tree of a wheel, etc. See GLOBE, WHEEL, etc.
Axis of the World, in astronomy.—The axis of the world is an imaginary right line, conceived to pass through the centre of the earth, and terminating at each end in the surface of the mundane sphere. See SPHERE.
About this line as an axis, the sphere, in the Ptolemaic system, is supposed daily to revolve. See EARTH and ROTATION.
See also PTOLEMAIC.
This axis is represented by the line PQ, Tab. Astronomy, Fig. 52.—The two extreme points hereof, in the surface of the sphere, viz. P and Q, are called its poles. See POLE.

Axis of the Earth, is a right line, upon which the earth performs its diurnal rotation. See EARTH, ROTATION, etc.
Such is the line PQ, Tab. Geography, Fig. 7.—The two extreme points hereof are also called poles. See POLE.
The axis of the earth is a part of the axis of the world. It always remains parallel to itself, and at right angles with the equator. See PARALLELISM.
Axis of a Planet, is a line drawn through the centre thereof about which the planet revolves. See PLANET, etc.
The sun, moon, and all the planets, except Mercury and Saturn, are known, by observation, to move about their several axes; and the like motion is easily inferred of those two. See SUN, MOON, MERCURY, SATURN, etc.
Axes of the Horizon, the Equator, Ecliptic, Zodiac, etc. are right lines drawn through the centres of those circles perpendicularly to the planes thereof. See CIRCLE. See also HORIZON, ECLIPTIC, EQUATOR, etc. See also PLANE, etc.
Axis, in mechanics—The axis of a balance is the line upon which it moves or turns. See BALANCE. Axis of Oscillation, is a right line parallel to the horizon, passing through the centre, about which a pendulum vibrates. See OSCILLATION and PENDULUM.
Axis, in geometry.—Axis of Rotation, or Circumvolution, is an imaginary right line, about which any plane figure is conceived to revolve, in order to generate a solid. See SOLID, GENESIS, etc.
Thus a sphere is conceived to be formed by the rotation of a semicircle about its diameter or axis, and a right cone by that of a right angle triangle about its perpendicular leg, which is here its axis.
Axis of a Circle or Sphere, is a line passing through the centre of a circle or sphere, and terminating at each end, in the circumference thereof. See CIRCLE and SPHERE.
The axis of a circle, etc. is otherwise called the diameter thereof—Such is the line AB, Tab. Geometry, Fig. 27. See DIAMETER.
Axis is yet more generally used for a right line proceeding from the vertex of a figure to the base thereof. See FIGURE, VERTEX, and BASE. Axis of a cylinder is properly that quiescent right line about which the parallelogram turns, by whose revolution the cylinder is formed. See CYLINDER.
Though, both in right and oblique cylinders, the right line joining the centres of the opposite bases, is also called the axis of the cylinder.
Axis of a Cone is the right line or side upon which the right angled triangle forming the cone makes its motion. See CONE. Hence it follows that only a right cone can properly have an axis; in regard an oblique one cannot be generated by any motion of a plane figure about a right line at rest.
But in regard the axis of a right cone is a right line drawn from the centre of its base to the vertex; in analogy hereto the writers of conics do likewise call the same line drawn from the centre of the base of an oblique cone to the vertex, the axis thereof. Axis of a vessel, is that quiescent right line passing through the middle thereof, perpendicularly to its base, and set distant from its sides. Axis of a conic section, is a right line passing through the middle of the figure, and cutting all the ordinates at right angles. See CONIC SECTION.
Thus if AP, Tab. Conics, Fig. 31. be drawn perpendicularly to MN, so as to divide the conic into two equal parts, it is called the axis of the section. See SECTION.
Transverse Axis, called also the first or principal axis of an ellipse or hyperbola, is the axis AP, last defined: being thus called in contradistinction to the conjugate or secondary axis.
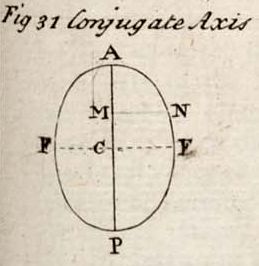
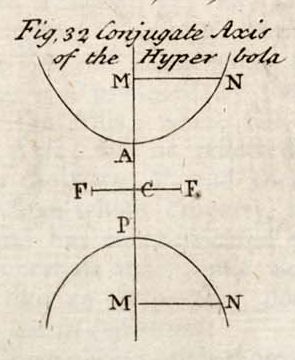
The transverse axis in the ellipse is the longest; in the hyperbola it cuts the curve in the centre. The conjugate axis, or second axis of the ellipse, is the line FF, Fig. 32. drawn through the centre of the figure C, parallel to the ordinate MN, and perpendicularly to the transverse axis; being terminated at each extreme by the curve. See ELLIPSIS.
The Conjugate is the shorter of the two axes of an ellipse. See CONJUGATE.
Conjugate, or second Axis of a hyperbola, is the right line FF, Fig 32. drawn through the centre parallel to the ordinates MN; MN, perpendicularly to the axis AP.

See HYPERBOLA. The length of this axis, though more than infinite, may be found by this proportion, √(AM x PM) : AP :: ²MN: FF.
Axis of a Parabola, see PARABOLA. The axis of a parabola is of an indeterminate length, that is infinite. The axis of the ellipse is determinate—The parabola has only one axis; the ellipse and hyperbola two. See CURVE.
AXIS IN OPTICKS—Optick Axis, or Visual Axis, is a ray passing through the centre of the eye; or it is that ray which proceeding out of the middle of the luminous cone, falls perpendicularly on the crystalline humour, and consequently passes through the centre of the eye. See OPTICK, RAY, CONE, VISION.
Common or mean axis, is a right line drawn from the point of concurrence of the two optick nerves; through the middle of the right line, which joins the extremity of the same optick nerves. See OPTICK NERVE.
Axis of a Lens, or Glass, is a right line passing along the axis of that solid whereof the lens is a segment.
See LENS and GLASS.
Thus a spherical convex lens, being a segment of some sphere; the axis of the lens is the same with the axis of the sphere; or it is a right line passing through the centre thereof. See CONVEX, etc. Or the axis of a glass is a right line joining the middle points of the two opposite surfaces of the glass. See OPTICK GLASS.
Axis of Incidence, in Dioptricks, is a right line drawn through the point of incidence, perpendicularly to the refracting surface. See INCIDENCE.
Such is the line DB, Tab. Opticks, Fig. 56.
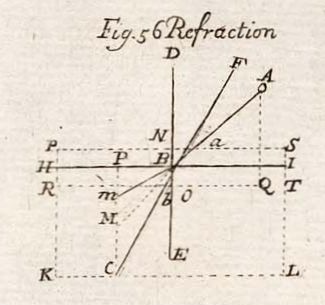
Axis of Refraction, is a right line continued from the point of incidence or refraction, perpendicularly to the refracting surface, along the further medium.—Such is the line BE. Or it is that made by the incident ray, perpendicularly projected on the side of the second medium. See REFRACTION.
Axis of a Magnet, or Magnetical Axis, is a line passing through the middle of a magnet, lengthwise; in such manner, as that however the magnet be divided, provided the division be according to a plane wherein such line is found, the lodestone will be made into two lodestones. See MAGNET and MAGNETISM. The extremes of such lines are called the poles of the stone. See POLE and POLARITY.
Axis, in anatomy, is the third vertebra of the neck; reckoning from the skull. See VERTEBRA. It is thus called by reason the two first vertebrae, with the head, move thereon, as on an axis. See HEAD and NECK.
Spiral Axis, in architecture, is the axis of a twisted column, drawn spirally, in order to trace the circumvolutions without. See TWISTED COLUMN. Axis of the Ionick Capital, is a line passing perpendicularly through the middle of the eye of the volute. See IONIC and VOLUTE. The axis is otherwise call’d cathetus. See CATHETUS.
Axis in Peritrochio, is one of the five mechanical powers, or simple machines; contrived chiefly for the raising of weights to a considerable height. See MECHANICAL POWER, etc.
It consists of a circle, represented AB, (Tab. Mechanicks, Fig. 44.) concentric with the base of a cylinder, and moveable together with it, about its axis EF—This cylinder is called the axis, the circle, the peritrochium; and the radii, or spokes, which are sometimes fitted immediately into the cylinder, without any circle, the scytale.
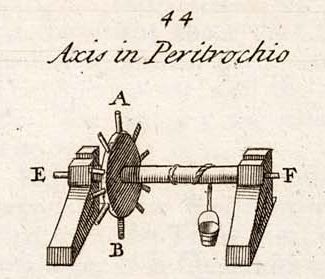
See PERITROCHIUM.
Round the axis winds a rope, whereby the weight, etc. is to be raised.
The axis in peritrochio takes place in the motion of every machine, where a circle may be conceived described about a fixed axis, concentric to the plane of a cylinder about which it is placed; as in crane-wheels, mill-wheels, capstans, etc. See WHEEL.
Doctrine of the Axis in Peritrochio. 1. If the power, applied to an axis in peritrochio, in the direction AL, Fig. 7. perpendicular to the periphery of the wheel, or to the spoke, be to a weight G, as the radius of the axis CE, is to the radius of the wheel CA, or the length of the spoke; the power will just sustain the weight, i.e. the weight and the power will be in equilibrio.
2. If a power be applied to the wheel in F, according to the line of direction FD, which is oblique to the radius of the wheel, though parallel to the perpendicular direction; it will have the same proportion to a power which acts according to the perpendicular direction AL, which the whole sine has to the sine of the angle of the direction DFC.
Hence; since the Distance of the Power in A is the Radius CA; the Angle of Direction DFC being given; the Distance DC is easily found.
Powers applied to the Wheel in several Points; F and K; according to the Directions, FD and KI, parallel to the perpendicular one AL, are to each other as the Distances from the Centre of Motion CD and DI, reciprocally. Hence, as the Distance from the Centre of Motion increases; the Power decreases; and vice versa.—Hence also, since the Radius AC is the greatest Distance, and agrees to the Power acting according to the Line of Direction; the perpendicular Power will be the smallest of all those able to sustain the Weight G, according to the several Lines of Direction.
If a Power acting according to the Perpendicular AL, lift the Weight G; the Space of the Power will be to the Space of the Weight, as the Weight to the Power. For, in each revolution of the Wheel, the Power passes through its whole Periphery; and in the same time the Weight is raised a Space equal to the Periphery of the axis: The Space of the Power, therefore, is to the Space of the Weight, as the Periphery of the Wheel to that of the Axis: But the Power is to the Weight as the Radius of the Axis to that of the Wheel. Therefore, etc.
A Power; and a Weight being given, to construct an Axis in Peritrochio, whereby it shall be sustained. Let the Radius of the axis be big enough to support the Weight without breaking. Then, as the Power is to the Weight, so make the Radius of the Wheel, or the Length of the Spokes to the Radius of the Axis. Hence, if the Power be but a small part of the Weight, the Radius of the Wheel must be vastly great—E. gr. Suppose the Weight 3000, and the Power 50, the Radius of the Wheel will be to that of the Axis as 60 to 1.
This Inconvenience is provided against by increasing the number of Wheels and Axes; and making one turn round another by means of Teeth or Pinions. See WHEEL.
