The Word is compounded of the privative Particle α, συν, with, and πζοω, I fall ; g.d. In-coincident, or which never meet.—Some Latin thors call them Lineae Intactae.
Bertinus gives us divers sorts of Asymptotes; some Strait, others Curve; some Concave, others Convex, etc. and further, proposes an Instrument to describe them withal—Though, in strictness the Term Asymptotes seems appropriated to right lines.
Asymptotes, then, are properly right Lines, which approach nearer and nearer to some Curve, of which they are said to be the Asymptotes; but which, though they and their Curve, were indefinitely continued, would never meet. See CURVE.
Asymptotes may be conceived as Tangents to their Curves at an infinite Distance. See TANGENT. Two Curves are also said to be Asymptotical, when they thus continually approach, without a possibility of meeting —Thus, two Parabolas, whose Axes are in the same straight Line, are Asymptotical to one another.
Of Curves of the second Kind, that is, the Conic Sections, only the Hyperbola has Asymptotes, which are two in Number. All Curves of the third Kind have at least one Asymptote, but they may have three; and all Curves of the fourth Kind may have four Asymptotes. See CURVE OF HIGHER KIND. The Conchoid, Cissoid, and Logarithmic Curve, though not reputed Geometrical Curves, have each also one Asymptote. See MECHANICAL, TRANSCENDENTAL, etc.
Asymptote of the Conchoid
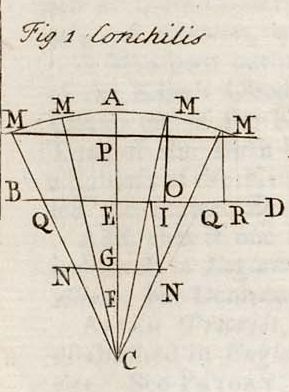
—The Nature of Asymptotes will be easily conceived in the Instance of the Asymptote of a Conchoid—Suppose MMAM, etc.
(Tab. Analysis, Fig. 1.) be a Part of a Conchoid, C its Pole, and the right Line Bd, so drawn that the Parts QM, EA, OM, etc. of right Lines drawn from the Pole C, are equal to each other: Then will the Line BD be an Asymptote of the Curve: Because the Perpendicular MI, etc.
is shorter than MO, and MR than MQ, etc. so that the two Lines continually approach; yet the Points M, etc. and R, can never coincide, in regard there is still a Portion of a Line to keep them asunder; which Portion of a Line is infinitely divisible, and consequently must be diminished infinitely ere it become nothing. See DIVISIBILITY, INFINITE, etc.
See also CONCHOID.
Asymptotes of the Hyperbola are thus described.
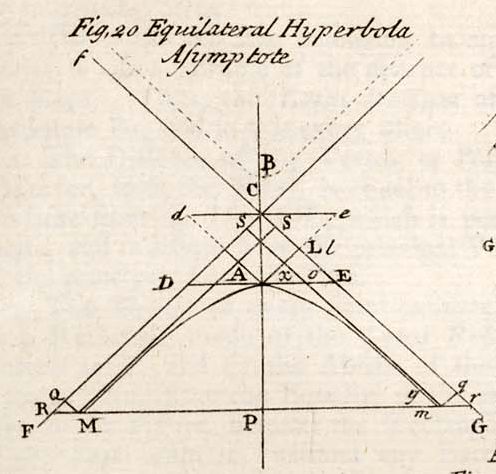
—Suppose a right Line DE (Tab. Conicks, Fig. 20.) drawn through the Vertex A of the Hyperbola, parallel to the Ordinates Mm, and equal to the Conjugate Axes, viz. the Part DA, and that AE to the Semi-axis: Then, two right Lines drawn from the Centre C, of the Hyperbola, through the Points D and E; viz. the right Lines CF and CG, are Asymptotes of the Curve. For the Properties of the Asymptotes of a Hyperbola, see HYPERBOLA.
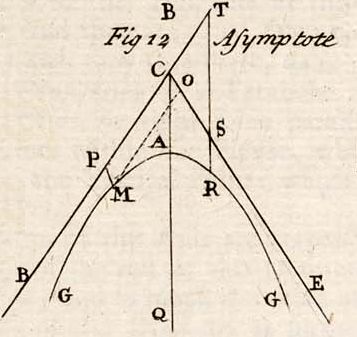
If the Hyperbola GMR, Fig. 12. be of any kind whose Nature with regard to the Curve and its Asymptote, is expressed, by this general Equation x^n y^n = a^n+b^n; and the right Line PM be drawn anywhere Parallel to the Asymptote CS, and the Parallelogram PCOM, be completed: This Parallelogram is to the hyperbolic Space PMGB, contained under the determinate Line M, the Curve of the Hyperbola GM indefinitely continued towards G, and the Part PB of the Asymptote indefinitely continued the same way, as m−n is to n: And so if m be greater than n, the said Space is squareable; but when m=n, as it will be in the common Hyperbola, the Ratio of the foregoing Parallelogram to that Space is as 0 to 1; that is, the Space is infinitely greater than the Parallelogram, and so cannot be had: And when m is less than n, the Parallelogram will be to the Space, as a negative Number to a positive one, and the said Space is squareable, and the Solid generated by the revolving of the indeterminate Space GMOL about the Asymptote CE; is double of the Cylinder generated by the Motion of the Parallelogram PCOM about the Axis CO. Asymptote of a Logarithmic Curve—If MS be the Logarithmic Curve, PR an Asymptote, PT the Subtangent, and MP an Ordinate; then will the indeterminate Space RPMS=PM+ PT²; and the Solid, generated by the Rotation of this Curve about the Asymptote VP, will be + of a Cylinder, whose Altitude is equal to the Length of the Subtangent, and the Semidiameter of the Base equal to the Ordinate QV. See LOGARITHMIC. ASYMPTOTIC Spaces. See HYPERBOLA.
